CM認知率の上限値は何パーセントか？〜「テレビコマーシャルカルテ」より〜

※本記事は2002年に発刊したVR Digestに掲載されたものです。

日頃"広告の効果"について「15秒CMと30秒CMの違い」「有効フリークエンシー」などいろいろご質問を頂くのですが、先日「CM認知率の上限値は何パーセントなのか？」という質問を初めて頂きました。確かに「理論上100％」ということは動かざる事実で議論する余地などないのですが、"現実としての上限値"となると「100％でいいのか？」と言われれば「100％ではなさそうだ」と答えざるを得ないような気がいたします。

図1は、横軸を「CM投下量」、縦軸を「CM認知率」として両者の関係を表したものです。出稿量が多くなるとCM認知率の伸びは鈍くなり、やがて飽和状態となり、それ以上は認知率が上がらない上限値に達する。そしてその上限値は100％以下になると考えられます。

図1：CM投下量とCM認知率の関係グラフ

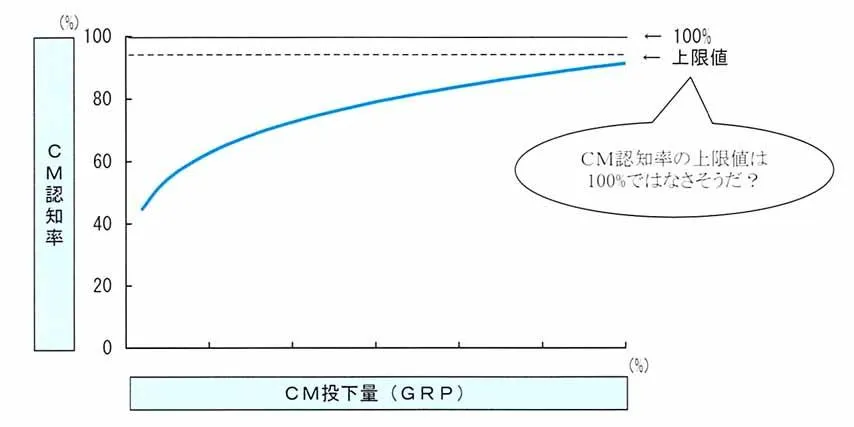
この"CM認知率の上限値"を考えるにあたり、今回は「調査結果からみた上限値」「回帰曲線モ

デルにより推定される上限値」の2つの側面からアプローチしてみることにしました。

◆90％そこそこ

これまで実際に記録されたCM認知率の最高値は何パーセントなのでしょうか。表1は、PM個人視聴率調査開始後の1997年4月から日件の12月までテレビコマーシャルカルテで調査されたCM4,01素材を対象にCM認知率をランキングしたものです。ターゲットは個人全体です。これによると、これまで実際に獲得されたCM認知率の最高値は92.6％（永谷園「お茶漬け海苔」）ということになります。このCM、確かにみなさんご存じかと思います。松村雅史（某広告代理店の社員という噂）という若い男性が、電話が鳴っているにもかかわらず「ただいまお茶づけ中」といって汗をかきながらお茶漬けをもの凄い勢いで掻き込むあのCMです。出稿量をみると世帯GRPで7,74GRPですからもうほぼ"打ち切った"いうレベルかと思いますが、リーチは98.5％なのでもうちょっと（本当に"もう少し"）認知率は上がるかも知れません。その次にCM認知率の高かったサントリー「ダイエット」は、つい最近まで放送されていたCMなのでもっと記憶に新しい（同様のシリーズCMはまだオンエア中）と思います。こちらは出稿量が1,466GRP（世帯GRP）、リーチは92.5％なので永谷園「お茶漬け海苔」よりもまだ認知率拡大の可能性を秘めているCMと言えるでしょう。

また図2の「CM認知率の度数分布」をみると、CM認知率90％以上のCMは僅か0.1％、1000CMに1つの割合でしか存在しません。先ほどのCM認知率の最高値92.6％と併せて考えると、「調査結果からみたCM認知率の上限値は"90％そこそこ（92.6％＋α）"のレベルではないかと推測できます。

表1：テレビコマーシャルカルテにおける CM認知率ランキング（個人全体）

＜VOL.90（1997年4月調査）〜VOL.147（2001年12月調査）対象CM＞

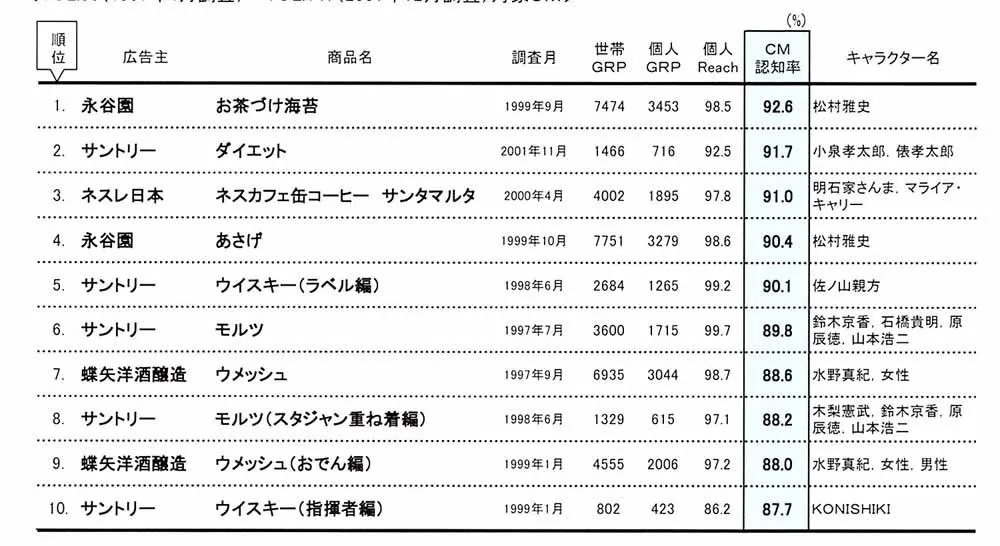
※ランキング対象は、個人全体のReachが50％以上のCM素材。GRPはすべて本数ベース。

図2：テレビコマーシャルカルテにおける CM認知率の度数分布（個人全体）

＜VOL.90（1997年4月調査）〜VOL.147（2001年12月調査）対象＞

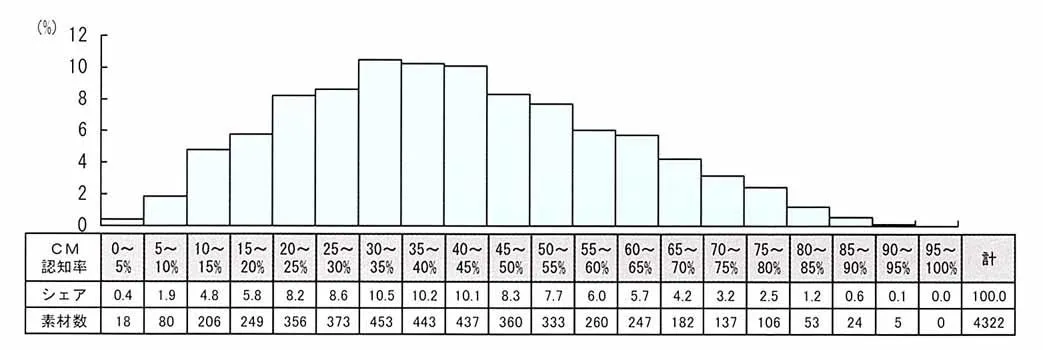
※個人全体のReachが50％以上のCM素材を対象。

◆今は存在しない上限値

調査結果からだけでは、"90％そこそこ"という暖味な値でしかCM認知率の上限値を推測できないので、ここからはもう少し理論的に上限値を考えていきたいと思います。

図3は、当社が「テレビコマーシャルカルテスペシャルレポート」で発表している「CM投下量とCM認知率の関係」です。通称「Nom曲線」といわれています。この関係式は「べき乗回帰曲線（y＝ax^b、y：CM認知率、x：個人GRP）」で表され、y（CM認知率）の極限値（上限値）は設定されないモデルとなっています。「スペシャルレポート2000」で発表したNom曲線（全業種、個人全体）では9,869GRP（個人GRP）でCM認知率100％に達し、それ以上の出稿では推定される認知率が100％を越えてしまいます。

図3：CM投下量（個人GRP）とCM認知率の関係（全業種、個人全体）

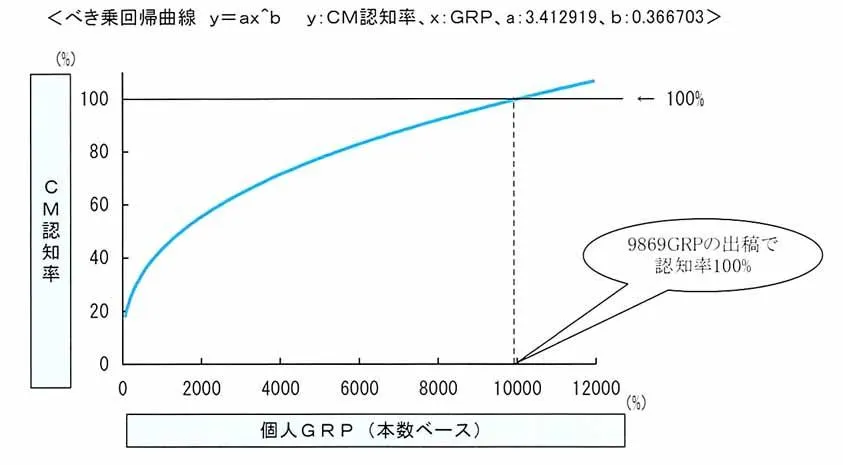
※「TV−CM KARTE Special report 2000」より

本来、認知率が100％を越えることはあり得ないので、べき乗回帰曲線を「CM投下量とCM認知率の関係」に用いるのは間違いかもしれませんが、これには大きく2つの理由があります。

一つは、他の回帰曲線モデルよりも当てはまりの精度がやや良いということです。べき乗回帰は、CM認知率の上限値や原点を通ること（出稿量が0の時はCM認知率も0％となること）を考慮せず（縛りが少なく）自由に回帰モデルを当てはめるのでやや精度がよくなります。Nom曲線を発表する意図が「出稿量に対するCM認知率を理論的に推測する」という研究的な視点よりは、むしろ「出稿量に対する標準的なCM認知率を計る」というところにあり、調査結果から平均値を算出するという点に重きを置いているからです。したがって、「理論的にCM認知率が100％を越えることはあっても、精度の良い標準的なCM認知率が推測できればよい。その方が実務上の利用度が高い」と思われるためです。

2つ目の理由は、「求められたべき乗回帰モデルからCM認知率が100％になる出稿量（GRP）を算出すると、現実には考えられないような膨大な出稿量が必要になる」ということです。先ほど図3でCM認知率100％に達するには9，869GRP（個人GRP）の出稿が必要と書きましたが、これは世帯GRPに換算すると2万GRP近くも必要ということになり、現実には考えにくいレベルです。表2は、表1と同様の4，401CMを対象にした出稿量（個人GRP）ランキングです。これまで実際に最も多く出稿されたCMでも個人GRPで6，308GRPと、CM認知率が100％を越えるようなレベルで推定される出稿量ではありません。したがって、理論上CM認知率が100％を越えることがあっても、現実的には100％を越える認知率が推定されてしまって不便することはないと考えられるためです。

表2：テレビコマーシャルカルテにおける 出稿量（個人GRP）ランキング（個人全体）

＜VOL.90（1997年4月調査）〜VOL.147（2001年12月調査）対象CM＞

※ランキング対象は、個人全体のReachが50％以上のCM素材。GRPはすべて本数ベース。

◆理論上の上限値は97.4％！？

では、仮に上限値の設定できる回帰曲線モデルを「CM投下量とCM認知率の関係」に当てはめ、そこからCM認知率の上限値を推定することはできないでしょうか。

上限値の設定できる回帰曲線モデルには、「修正指数曲線」「ロジスティック曲線」「ゴンペルツ曲線」などの成長曲線があります。これらモデルの違いなど詳しい説明は割愛させて頂きますが、ここでは「CM投下量とCM認知率の関係」に理論上最も当てはまりの良いであろう「ゴンペルツ曲線」を用いてCM認知率の上限値を考察していきたいと思います。

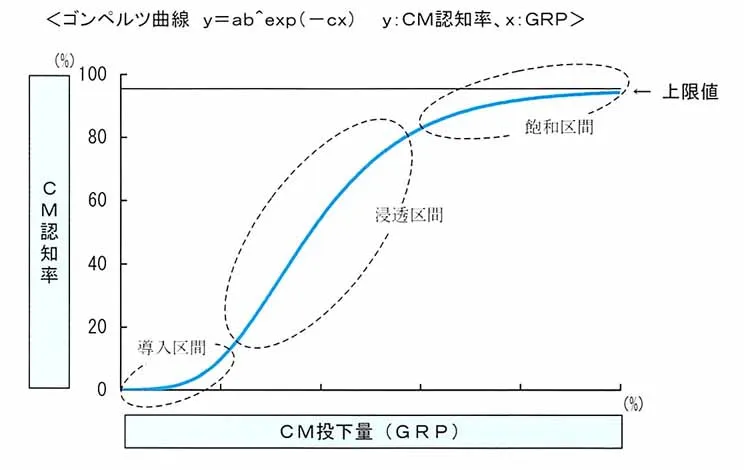
図4は「CM投下量とCM認知率の関係」を「ゴンペルツ曲線（y＝ab^exp（-cx）、y：CM熟知率、x：個人GRP）」で表したものです。出稿量が少ないあるレベルまではCM認知率の伸びは鈍いものの（導入区間）、それを越えると急激に認知率は増加し（浸透区間）、その後再び伸びが鈍くなり（飽和区間）、最終的にある一定レベルで認知率は上限値に達します。これは、「出稿量が増えると徐々にCM認知率の伸びが鈍くなる」という単縄なべき乗回帰曲線の考えから一歩踏み込み、「ある一定回数以上接触しないとCMは認知してもらえないが（導入区間）、その後一定回数以上接触するとCMは認知され始める（浸透区間）」という有効フリークエンシーの考えを取り入れたかたちになります。

図4：ゴンペルツ曲線による CM投下量とCM認知率の関係グラフ

ではこの「ゴンペルツ曲線」を「テレビコマーシャルカルテスペシャルレポート2000」でNorm曲線の作成に用いたものと同じ調査素材に適用し、実際にモデルを算出してみます（全業種、個人全体）。算出にあたっては上限値（CM認知率の上限値）を任意に設定しなければいけないので、とりあえず上限値を96.0から100.0まで0.5刻みに設定してモデルを算出してみます。

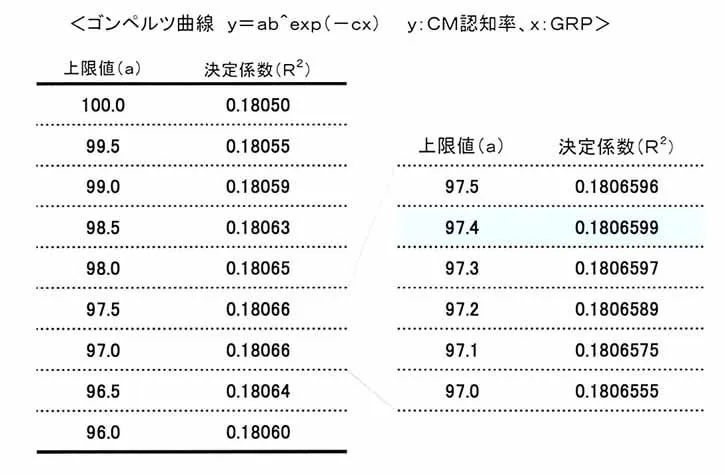
算出されたモデルの決定係数を比較して、最もモデルの精度が良くなる上限値を探すと「97.0」と「97.5」になりました（表3参照、決定係数が大きいほど精度が良い）。そこでさらに上限値の刻みを細かくしてモデルを算出し、決定係数を比較してみると、「97.4」の時にもっとも精度が良くなるということになりました（この考えは「くりかえし法」と呼ばれ、上限値（飽和点）を探すときに用いられる方法です）。したがって、このくりかえし法によれば「ゴンペルツ曲線により推定されるCM認知率の上限値」は"97.4％"ということになります（決定係数が全体に低いのが少々気になりますが...）。

表3：ゴンペルツ曲線における 上限値と決定係数の関係（個人全体）

※テレビコマーシャルカルテ関東地区VOL.l14〜140で調査を実施した2721素材で算出

以上2つの側面から"CM認知率の上限値"を探ってみましたが、何れのアプローチにせよ「100％ではなさそうだ」というのは確かなようです。CM認知率100％というのは、全ての人にTV−CMが接触してかつ覚えてもらうということですから、当然といえば当然の結果かも知れません。しかし逆に考えれば、TV−CMだけでも"90％そこそこ（92.6％＋α）"あるいは"97.4％"のレベルまで認知率が獲得できるということは、TVの媒体価値の高さを物語っている結果とも言えるでしょう。

（第一マーケティング局 メディアマーケティング部 長島英樹）